A member of a Discord server I moderate was curious about how to roll a tetrahedron. And that intrigued me. It’s such a unique problem. They wanted something similar to Tarodev’s “Roll-A-Cube” video.

Searching for a pre-existing solution to see if this had been done before turned up nothing. So I got to work. Engineering a solution to a unique problem involves trial and error, and I’ve purposefully included any non-working attempts so that you can follow along with the process.

For my initial approach, I’ll try modifying the Roll-A-Cube code, which uses the RotateAround method. But before we get to that, we’ll need a 3D model to work with.

# 3D Tetrahedron Model

The requirements I set for myself were the following:

• Edge length of 1 unit (a.k.a. “unit tetrahedron”).
• Bottom face is level with the XZ-plane (y = 0).*
• Top vertex is centered directly above the origin.
• Pointy end forward (though this can easily also point right, not a hard-set constraint).
• Precision is important so I can’t rely on downloading someone else’s model.

*Note: This was just for easier math; we will offset it later so the center is at the origin.

With this setup, I did the math (I will leave the fun of trigonometric computations to the reader) and came out with the following 4 vertices:

1
2
3
4

Back-left: (-0.5, 0, -0.288675)  // z = -sqrt(3)/6
Back-right: (0.5, 0, -0.288675)
Forward:    (0, 0, 0.577350)     // z = 1/sqrt(3)
Top:        (0, 0.816497, 0)     // y = sqrt(2/3)

All 4 vertices are 1 unit away from each other and sqrt(3/8) units away from the center:

1

 Center is at: (0, 0.2041241, 0) // y = sqrt(6)/12

If you want to try deriving it for yourself, I also recommend a linear algebra approach by setting up a few system of equations to solve for the unknowns. Alternatively, you can check out the Tetrahedron Wikipedia page for examples, and apply your desired scaling and offset.

With these 4 vertices, we can now create our mesh. How you choose to do this is up to you:

• 3D Modeling Software (i.e. Blender) - Benefits are: easier customizations like smoothing edges, UV/Texture maps, etc.
• ProBuilder in Unity - New Shape > Cone > Radius = 0.5773503, Height = 0.8164966, Sides = 3. Note: This didn’t feel as accurate and will require modified code to work with later because it’s not a regular Mesh but a ProBuilderMesh.
• Generate Mesh via code - I’ve created a script to generate it for you in one click. I purposefully offset the mesh vertices down so that the center is at the origin. This makes it easier for rotating.

Once you have the mesh generated, it’s time to set up the GameObject structure. It’s generally a good practice to keep the visuals separate from the logic. We’ll classify the rotation as part of the visuals, but the movement still needs to be applied to the root object. Set it up with the mesh as a child object, then gave the child’s local position the appropriate y-offset.

# RotateAround Approach

Transform.RotateAround requires 3 pieces of information:

• A Vector3 axis to rotate around
• A Vector3 point, a world-space anchor, for which the axis passes through
• A float angle of rotation in degrees

We need to access the world positions of the vertices to get the axis and point to rotate around. If you were to access the vertex info from the MeshRenderer’s Mesh data, they would be returned as local offsets. They can be converted to world coordinates with transform.TransformPoint(vertexOffset). Alternatively, we can add 4 Transforms as children, use vertex-snapping (by holding v) to position them, and add them to a List<Transform> _vertices, which is what I’ll use for this example.

Since we’re just prototyping for a proof-of-concept at this stage, quick iteration is more important than performance, so we can do a quick-and-dirty Linq statement:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

// in case input isn't already swizzled for 3D
var dir = new Vector3(horizontalInput, 0f, verticalInput);
// acts as our "carrot on a stick", used for a distance check
var target = transform.position + dir;
// given world position vertices, ignore top-most vertex and take the closest two
var closestVertices = _vertices.Where(v => v.position.y < 0.5f)
      .OrderBy(v => Vector3.Distance(v.position, target))
      .Take(2).ToArray();
// the direction of the axis vector is important for how RotateAround works
var axis = closestVertices[1].position - closestVertices[0].position;
// we can use the Cross Product to know if this will rotate correctly
if (Vector3.Cross(dir, axis).y < 0f) // the resulting vector should point upwards
   axis = -axis;
// either vertex (index 0 or 1) will work for the anchor point
var anchor = closestVertices[0].position;

Finally, we’ll need the angle of rotation. For a cube, it’s an easy 90°. But for a tetrahedron, it’s a bit harder to calculate. Spoiler alert: it’s 109.4712206..°, or acos(-1/3). According to the wiki page, this is the same as the “Vertex-Center-Vertex” angle. However, I initially solved it for the angle between two faces, also known as the “dihedral angle”, then subtracted that from 180°.

# RotateAround Results

So this will work. If performance is a concern, replace Linq with something that doesn’t generate garbage. If you’re happy with those results, you can stop reading here, grab the complete script, and enjoy the rest of your day. 🎊

But it does have some limitations to be aware of:

1. Over a long distance, after many rolls, some error will accumulate and the orientation won’t be perfectly flush. This is because the angle of rotation is an irrational number, and there will be floating point errors.
2. It’s not very easy to apply an easing function to alter the feel of the roll with RotateAround.

With those limitations in mind, what are some other potential ways to rotate a tetrahedron?

• Rigidbody & AddTorque - physics isn’t always reliable; we want more control over how it moves. ❌
• Hard-code all 6 possible orientations and their transitions - too inflexible, feels hacky, lots of work. ❌
• Get target rotations procedurally with raycasts and use quaternions - seems promising, let’s try it! ✔️

# Procedural Approach

The main issue we want to avoid from before is compounding errors. Every rotation should be independent and absolute. Meaning: if one rotation under- or over-shoots, the next should have a definitive target so that errors don’t add up. Previously, RotateAround handled both rotation and movement, so we’ll need to handle the movement part separately.

Here’s the plan:

1. The input direction will be used for a raycast to hit 1 of the faces.
2. We’ll use the normal of the triangle to loosely represent an orientation (no need to keep track of vertices anymore).
3. That face should end up on the bottom, where its normal will point down, so we calculate the required rotation to make that happen.
4. And then we’ll figure out movement later.

# Determining the Rotation

If we want to hit the correct face from the outside with a raycast, we’ll want to use a LayerMask to avoid other objects potentially intercepting that ray. Or… now hear me out… we start our raycast from the inside. By default, raycasts won’t hit the back-side of triangle faces. We can solve that in one of two ways: recreate the mesh so that the fronts of the triangles are visible from the inside (i.e. make it double-sided), or simply enable it with:

1

Physics.queriesHitBackfaces = true; // also found in Project Settings > Physics

I’m choosing this simpler option.

Side note: if you ever want to add a Rigidbody, Unity complains that the mesh isn’t “convex”. And if you tick the Convex checkbox on the Mesh Collider, the raycasts won’t detect the back faces for some reason.

If you’re unfamiliar with Quaternions, check out my other post explaining them! For now just know they represent rotations and/or orientations. They can interpolate more accurately than using Euler angles, always taking the shortest path, and aren’t subject to gimbal lock.

With the goal to rotate so that the hit face ends up on the bottom, we can get the target orientation with the following code:

1
2
3
4

// required rotation that gets us from A to B
var deltaRot = Quaternion.FromToRotation(hit.normal, Vector3.down);
// we know A already, this gives us B so that we can interpolate between the two
var targetRot = deltaRot * _center.rotation; // where _center is the child Transform

Note: The order of multiplying quaternions together matters. The left-hand-side will be applied to the right-hand-side.

# Determining the Movement

To figure out how far we need to move, that’s just twice the distance from the center of an equilateral triangle to the middle of an edge. The total distance is 1/sqrt(3), so we can make that a variable:

1

private const float ONE_OVER_ROOT_THREE = 0.5773503f;

To get the direction, we can use the normal again and just zero-out the y-component and normalize it:

1

var moveDir = new Vector3(hit.normal.x, 0f, hit.normal.z).normalized;

The end position after a full rotation will be:

1

var targetPos = transform.position + ONE_OVER_ROOT_THREE * moveDir;

It’s worth mentioning that there is still a chance for some positional error accumulation. If you have a very large map where the position needs to be accurate to a grid, you’ll want to grab the coordinates from the grid cell instead. You can set up your own coordinate system or just raycast the ground triangle and cleverly use hit.barycentricCoordinate. But this will work for our purposes without over-engineering.

# Interpolating/Tweening

Now that we have figured out our targets for rotation and movement, we need to interpolate. There are many options to achieve this:

• Your choice of tweening library if they support quaternion rotations
• Create a coroutine utilizing any of the following
  • Lerp
  • Slerp
  • RotateTowards / MoveTowards

Since we’re still prototyping, I will start out with DOTween. It’s basically a coroutine without having to write all of the boilerplate, and it’s free from the asset store.

# DOTween

Rotating is as simple as calling this one line:

1
2

// _timeToMove is a shared float for moving and rotating. 0.5f seconds worked fine
transform.DORotateQuaternion(targetRot, _timeToMove); // bonus: add .SetEase(Ease.OutSine)

Note: DOTween suggests to use DORotate, but don’t; that method uses euler angles and we know how that turns out.

We also need to move our object up then down smoothly as it moves. Fortunately, DOTween has our back with:

1

transform.DOJump(targetPos, _jumpPower, 1, _timeToMove);

After tweaking the _jumpPower to stay in contact with the ground, a value of ⅙ was good enough: 0.166f

It looks promising! However… there’s one small detail that I don’t like…

It doesn’t stay anchored.

# Coroutine with Slerp

The rotation in the coroutine also requires that we first cache the start so that we can properly Slerp between the start and target.

1
2
3
4
5
6
7

/* Coroutine setup */
var deltaRot = Quaternion.FromToRotation(hit.normal, Vector3.down);
var startRot = _center.rotation;
var targetRot = deltaRot * startRot;

/* Applied every frame in the coroutine */
_center.rotation = Quaternion.Slerp(startRot, targetRot, t);

If you’ve never used Vector3.Slerp before, think of it like a windshield wiper. A vector gets rotated from pointing in one direction to pointing in another. With that in mind, we need to mainly work with offsets, which we then add onto a world position reference point - an anchor.

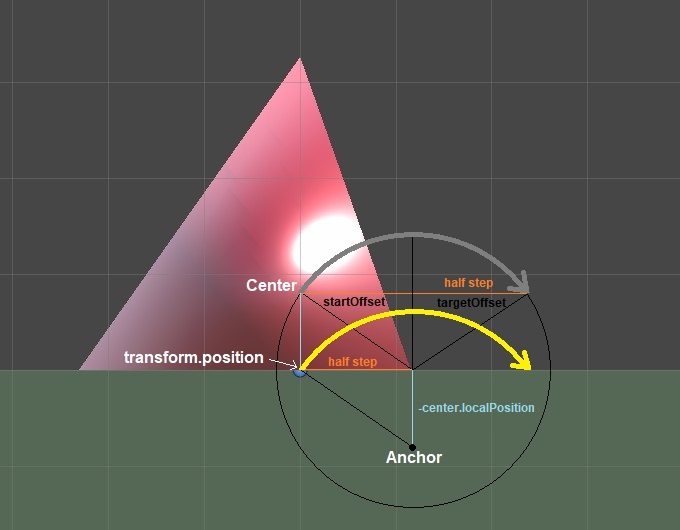
In this diagram, the Slerp operation would move a vector along a circular path, depicted by the gray arrow. To achieve moving the parent (transform.position) along the yellow curved path, this is the relevant parts of the movement code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

/* Declared at the top */
private const float ROOT_THREE_OVER_SIX = 0.288675135f; // half the previously-declared const

/* Coroutine setup */
var moveDir = new Vector3(hit.normal.x, 0f, hit.normal.z).normalized;
var halfStep = ROOT_THREE_OVER_SIX * moveDir;
var startOffset = _center.localPosition - halfStep; // notice localPosition usage for offset
var targetOffset = _center.localPosition + halfStep;
var anchor = transform.position - startOffset;

/* Applied every frame in the coroutine */
transform.position = anchor + Vector3.Slerp(startOffset, targetOffset, t);

And that’s it! With this approach, it’s very easy to add an AnimationCurve for a custom easing function and it doesn’t rely on a third-party asset.

You can grab the complete script here.

Happy rolling!